Grenzauflösung und MTF
Für den Bildverarbeiter ist es von Interesse, Objekte mit möglichst hoher Auflösung (Bildschärfe, Detailreichtum) und mit möglichst hohem Kontrast abzubilden. Das Bild sollte dabei grobe wie feine Objektstrukturen in allen Bereichen des Bildes wirklichkeitsgetreu darstellen. Dieser theoretische Wunschgedanke ist leider in der Praxis nicht perfekt umsetzbar. Es zeigt sich, dass besonders bei feinen Objektstrukturen Kontrastverschlechterungen auftreten, so dass ab einer gewissen Feinheit die Merkmale nicht mehr von der Software auswertbar sind. Diese Verschlechterung der Bildqualität nimmt typischerweise zusätzlich von der Bildmitte zum Bildrand zu.
Zur Beurteilung des Auflösungsvermögens der Optik wird in erster Linie die Modulationstransferfunktion (MTF) hinzugezogen. Diese vom Hersteller erhältlichen Diagramme treffen eine Aussage darüber, wie viele nebeneinander liegende schwarzweiße Linienpaare mit welchem Kontrast noch differenziert abgebildet werden – das heißt, je mehr Linienpaare bei möglichst hohem Kontrast, desto besser ist das Objektiv.
Doch was steckt dahinter?
Phänomen der Kontrastabnahme
Ausgangspunkt ist ein Testchart mit zunehmend feiner werdender Strukturierung von schwarz-weißen Balken (Linienpaare pro Millimeter) mit einem idealen, maximalen Objektkontrast von 100%. Anschließend kann im abgelichteten Bild der resultierende Kontrast der einzelnen Hell-Dunkel-Muster erneut gemessen werden:
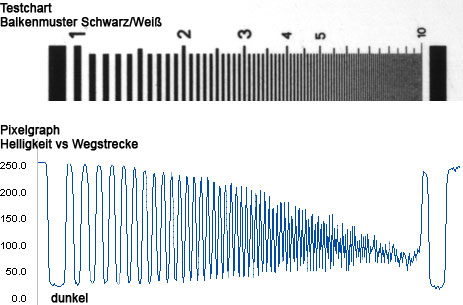 |
Es zeigt sich, dass mit zunehmend feineren Objektstrukturen der Kontrast im Bild stetig abnimmt. Kantenpaare, die anfangs als schwarz-weiß zu bezeichnen waren, sind später nur noch dunkelgrau-hellgrau.
Bei der Abbildung dieser Testvorlage werden die Strukturen mit zunehmender Feinheit und gewöhnlich auch zum Bildrand hin „flauer“. Die höchste optische Leistung eines Objektivs liegt üblicherweise in der Bildmitte. Die feinsten Strukturen, die gerade noch mit einem "gewissen" Restkontrast zu erkennen sind, stellen die Auflösungsgrenze der Optik dar. Je mehr Kontrast die Optik bei feinsten Strukturen liefert, desto besser ist sie.
Ein MTF-Diagramm trägt letztendlich den gemessenen Bildkontrast gegenüber Linienpaaren /mm auf. Aber auch andere Darstellungsformen sind möglich.
Optische Grenzauflösung
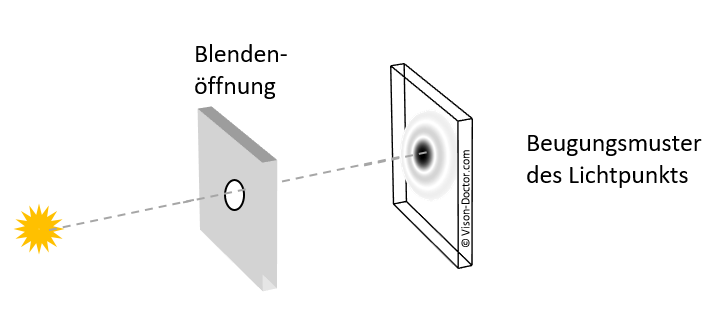
Ursache dieser Kontrastabnahme ist die Beugung des Lichts am Spalt. Aufgrund der Wellencharakteristik des Lichts, das als elektromagnetische Welle beschrieben werden kann, treten hier besondere Effekte auf. Trifft die elektromagnetische Welle des Lichts auf ein Hindernis, entsteht an der Kante eine neue Wellenfront, die sich auch in den geometrischen Schattenraum des Hindernisses ausbreiten kann. Bei Objektiven ist diese "Kante" die kreisförmige Blende der Optik, die dabei entstehenden Beugungsmuster sind konzentrische Intensitätsverteilungen.
 |
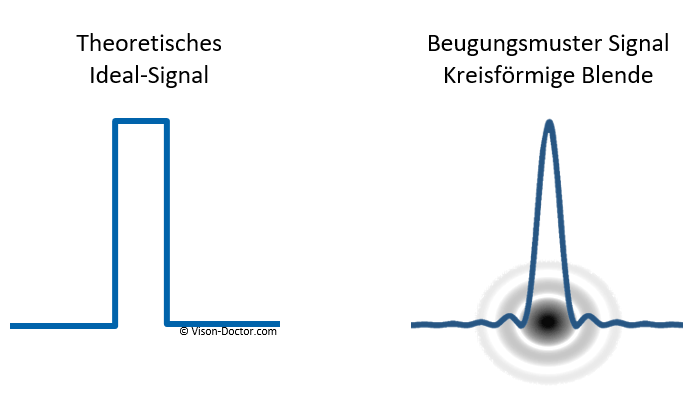
Aus dem theoretischen Ideal-Signal entsteht eine Intensitätsverteilung, die im Wesentlichen eine Besselfunktion erster Ordnung ist. Dieses Beugungsmuster wird auch airy disk genannt.
 |
Wird die Blende zunehmend geschlossen, kommt es zu einer Überlagerung der Beugungsscheibchen. Die Signal-Überlappung führt zur Abnahme des idealen theoretischen Schwarz-Weiß-Kontrasts unseres Testcharts. Je näher sich die zwei Signale annähern, desto geringer wird der Kontrast im Bild:
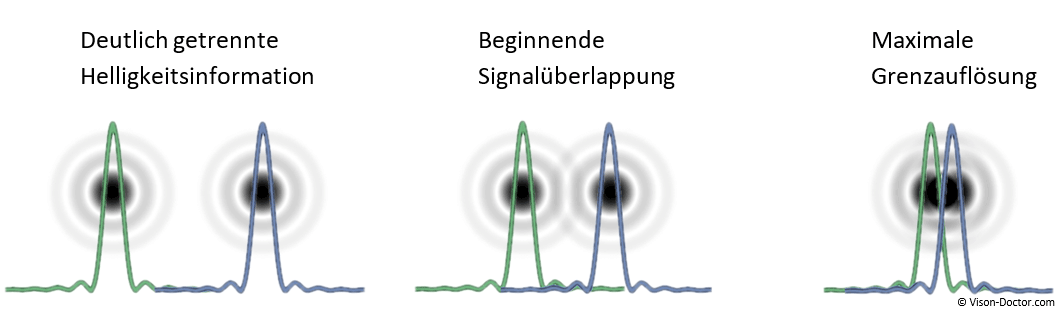 |
Beim Rayleigh-Kriterium geht man davon aus, dass sich zwei Beugungsscheibchen gleicher Intensität und Farbe noch trennen lassen, wenn das Minimum der ersten Nebenbeugung mit dem Maximum der zweiten zusammenfällt. Zwischen den beiden sich überlappenden Beugungsscheibchen fällt die Helligkeit auf 75 % des Maximalwertes ab. Dies entspricht immerhin noch einem Restkontrast von rund 14 % (des Ausgangskontrasts). Zwei Punkte lassen sich nur dann gerade noch trennen, wenn in der Abbildung ihre Maxima mindestens um den Radius r des Beugungsscheibchens auseinander liegen. Bei geringeren Objektkontrasten und bei Messapplikationen ist diese Aussage aber eher kritisch zu bewerten.
Als beugungsbedingte Grenzauflösung der kann der Durchmesser des Beugungsscheibchens verwendet werden. Hier sind die Signal-Peaks der Beugungsmuster noch kaum überlagernd, der Restkontrast noch entsprechend hoch. Gerade bei nicht idealen Ausgangsbedingungen, wo nicht immer 100% Ausgangskontrast vorliegt, ist dies eine sinnvolle Annahme.
Der Radius des erste Neben-Minimums des Beugungsmusters an der kreisförmigen Blende errechnet sich aus:
Rmin1 = 1,22 * Wellenlänge des Lichts * effektive Blendenzahl
Der Durchmesser des Beugungsscheibchens ist also:
d= 2 * 1,22 * Wellenlänge des Lichts * effektive Blendenzahl
Der Durchmesser des Beugungsscheibchens und damit die theoretische, beugungsbedingte Grenzauflösung hängen also von der Wellenlänge, aber besonders extrem von der Blendenöffnung der Optik ab. Ab Blende 5,6 bis 8 sind diese Werte bereits größer als die Pixelstrukturen moderner digitaler Bildsensoren sind.
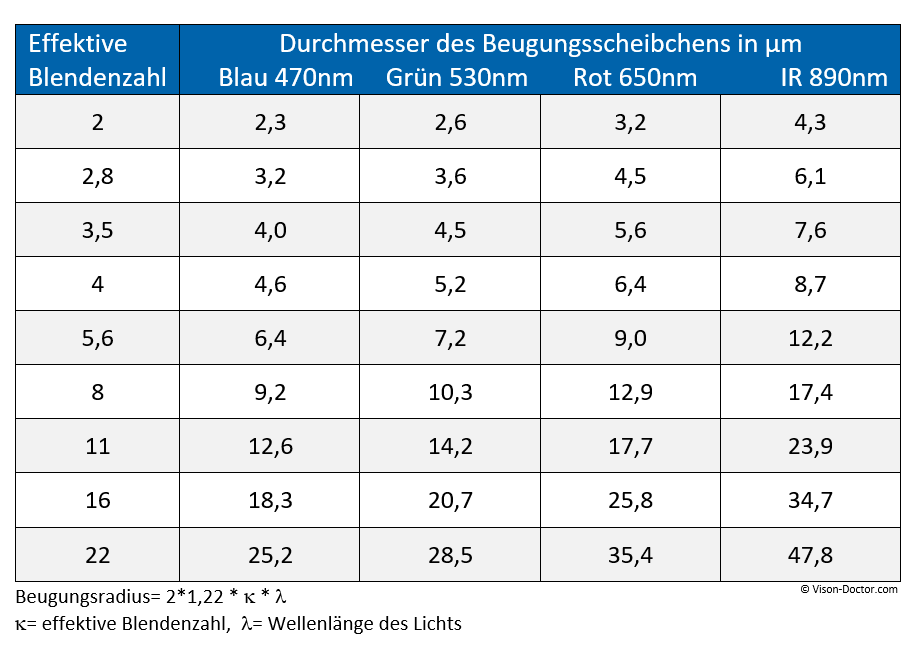 |
Ab Blende 5,6 bis 8 zeigt sich, dass diese Werte bereits größer als die Pixelstrukturen moderner digitaler Bildsensoren. Das Bildsignal wird auf mehrere benachbarte Pixel verschmiert, das Bild wird flau und unscharf.
Besonders eindrucksvoll zeigt sich dieser Effekt bei extrem starkem Abblenden der Optik:
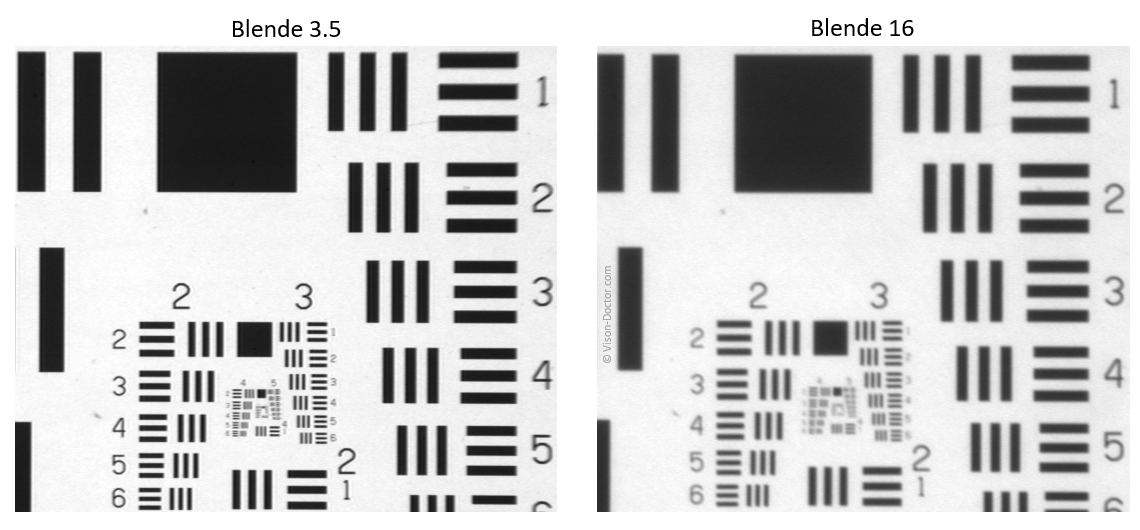 |
Trotz qualitativ hochwertiger Optik und Kamera zeigt sich eine extreme Bildverschlechterung beim Abblenden!
Die MTF-Kurve der Optik
Die Abbildungsleistung einer Optik wird in einem MTF-Diagramm angegeben. Diese ist stets geringer als die theoretische Begrenzung der Optik durch Beugungseffekte. Dabei wird die Strukturfeinheit (Linienpaare / mm) gegen den Bild-Kontrast aufgetragen (erste Abbildung).
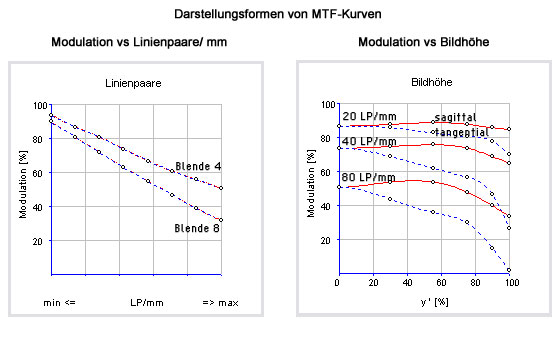 |
Neben dieser Darstellungsform kann die Modulation aber auch gegenüber der Bildhöhe dargestellt werden. Da sich vom optischen Zentrum bis hin zum Bildrand die Abbildungsleistung deutlich verschlechtert, wird diese Kontrastfunktion besonders gerne von Optik-Herstellern benutzt, und zwar in tangentialer Richtung, wie auch sagittaler (=radialer) Richtung zum optischen Zentrum der Linse.
Prinzipiell gilt:
- je höher die Modulationskurven ausfallen, desto besser ist das Objektiv
- je näher tangentiale und sagittale Kurven beieinander liegen, desto besser ist die Abbildungsleistung.
- Fällt in einem Bereich die Modulation unter 20%, ist die Optik in diesem Bereich wahrscheinlich für die Inspektion nicht mehr geeignet.
Achtung: Diese Werte beziehen sich alleine auf die optische Abbildungsleistung der Optik. Zur Betrachtung der MTF des gesamten Systems muss die MTF der Kamera mit der MTF der Optik verrechnet werden!
Grenzauflösung des Sensors
Auch der Bildaufnehmer der Kamera beeinflusst wesentlich die Grenzauflösung des Gesamtsystems.
Die theoretische Auflösung eines Kamerasensors wird dabei durch die Nyquist-Frequenz beschrieben:
NyquistFrequenz= 1 / ( 2*Pixelgröße)
Es muss laut Nyquist-Abtasttheorem zum Sampling eines Signals mehr als die doppelte Frequenz gegeben sein, um sich dem Ausgangssignal sauber anzunähern. Analog gilt das Abtasttheorem auch genauso bei Bildern, wobei die Abtastfrequenz dann in Pixeln oder Linienpaaren/mm bestimmt werden kann.
Für die individuellen Pixelgrößen der Bildsensorik ergibt dies deutliche Unterschiede, wie viele Linienpaare pro Millimeter aufgelöst werden können, da die Pixelgrößen moderner Kamera-Sensoren in der industriellen Bildverarbeitung von ca. 3,5 bis 14µm reichen. Dies ergibt ein theoretisches physikalisches Auflösungsvermögen von 7 bis 28µm bei der Abbildung feinster Strukturen.
Doch dies alleine trifft nicht unbedingt eine Aussage über die Messgenauigkeit...
Kombinierte Grenzauflösung = Messgenauigkeit des Gesamtsystems?
Ein schwieriges Thema! Die Grenzauflösung der Optik und des Sensors sind zu multiplizieren, so dass die MTF des Gesamtsystems immer unter der Abbildungsleistungs-limitierenden MTF liegt. Dies kann die Nyquistfrequenz des Sensors, aber auch die MFT der Optik sein. Leider kann jedoch der normale Anwender selten selbst MTF-Kurven ermitteln und nur die Ergebnis-Bilder betrachten.
In der Praxis heißt dies jedoch, dass feinste Objektstrukturen und die Übergänge der Objektkanten leicht verschwommen abgelichtet werden. Im Bild zeigen sich prinzipiell immer an den Objektkanten leichte Grauverläufe, die diese Unschärfebereiche darstellen.
Noch feinere Strukturen als 5-7µm sind jetzt zwar nicht unbedingt mehr erkennbar, allerdings kann unter idealen Voraussetzungen genauer als dieser Wert mit Hilfe von Sub-Pixeling-Verfahren (mathematische Interpolationen der Grautöne) gemessen werden! Ein Faktor von 3 bis 4 kann durchaus nochmals an Genauigkeit gewonnen werden, dieser Faktor ist jedoch alleine abhängig von der Qualität des dahinter stehenden Algorithmus.
In diesem Fall zeigt sich wiederum, dass möglicherweise ein Sensor mit größeren Pixeln, der theoretisch eine schlechtere Nyquist-Frequenz hat und damit weniger Linienpaare pro mm auflöst, ein wesentlich genaueres Messergebnis liefern kann aufgrund höherer Full-Well-Kapazität und geringerem Sensorrauschen.
Fazit:
Holen Sie sich für solche Diskussionen unbedingt den Rat und das Know-how von Spezialisten. Viele wichtige Details für diese Diskussion sind nicht unbedingt Datenblättern zu entnehmen und hier ist absolute Produkt-Kenntnis nötig, um ähnliche Komponenten verschiedener Hersteller zu vergleichen und ideal zu kombinieren. Führen Sie selbst gründliche Versuche zur Messmittelfähigkeit durch!






