Optische Grundlagen - Berechnung der Optik
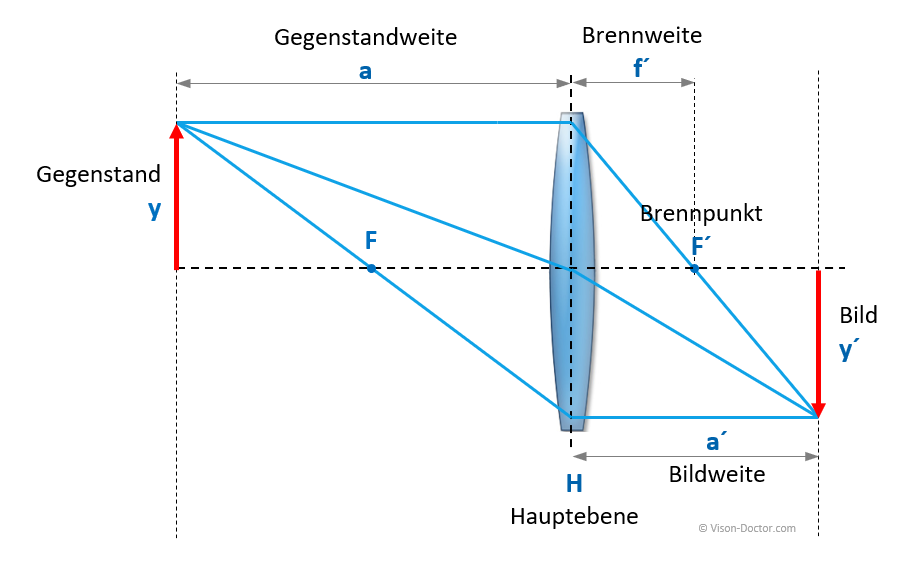
Die Berechnung der passenden Optik kann mit einfachen Formeln berechnet werden. Die dabei errechneten Resultate stellen jedoch nur Näherungswerte dar, da von einem einfachen Linsensystem (mit einer Hauptebene ausgegangen wird.
Trotzdem sind die einfachen Berechnungen meistens ausreichend genau, um je nach Bildfeld auf einige Zentimeter genau den Arbeitsabstand zu berechnen.
 |
In der Praxis spielen jedoch 4-7 Linsen(gruppen) zusammen, um die Abbildung möglichst fehlerfrei zu gestalten. Dieses komplexe Linsensystem weist zwei Hauptebenen auf, die gerechnete Gegenstandsweite ist die Entfernung bis zur ersten Hauptebene.
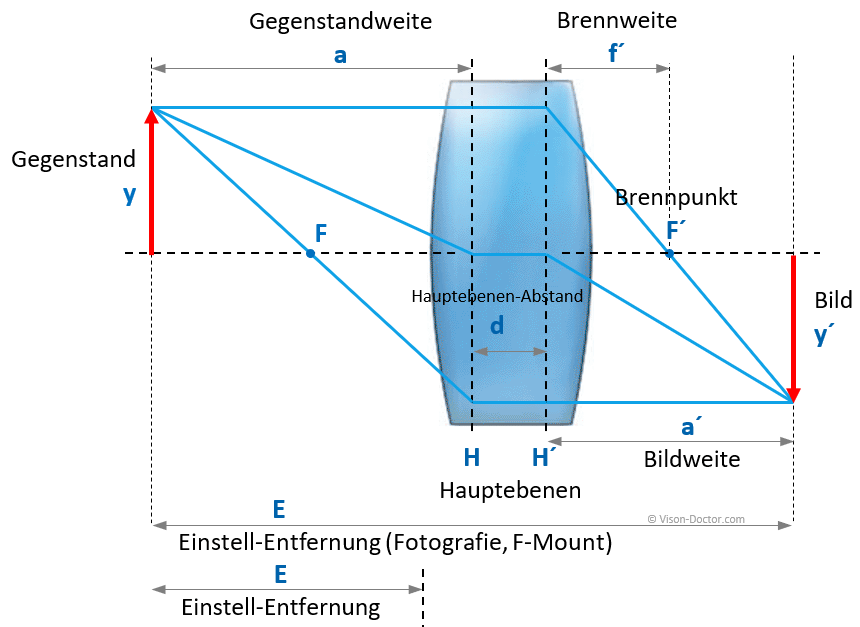 |
Die Gegenstandsweite ist daher genau genommen nicht der "Arbeitsabstand" bis zur Frontlinse des Objektivs, sondern liegt meist irgendwo in der Optik. Die Berechnung des "freien Arbeitsabstandes" bis zur Vorderkante des Objektivs kann nur exakt bestimmt werden, wenn die Länge des optischen Systems und die Lage der Hauptebenen bekannt ist. Oftmals liegen diese Objektivdaten dem Anwender nicht vor, so dass ein einfacher Kameratest nötig ist oder in der Praxis eine variable Kamerahöhenverstellung um einige Zentimeter eingeplant wird.
Die Einstellentfernung der Skala auf dem Objektiv ist bei C-Mount-Optiken die Distanz bis zur mechanischen Gehäusefront, bei Spiegelreflex-Optiken die Entfernung bis zur Filmebene.
Die wichtigsten Parameter zur Berechnung sind Bildfeld, Sensorgröße, Arbeitsabstand und Brennweite der Optik. Die ersten zwei Werte sind jedoch meist durch die Applikation fest definiert, so dass nur der Arbeitsabstand für eine bestimmte Brennweite, oder anders herum berechnet werden müssen.
Die Bildgröße y´ - Sensorgröße
Die Größe des Bildes y´ ist durch den Kamerasensor vorgegeben, muss also meistens nicht berechnet werden. Die Maße werden meist in Zollangaben gemacht, sind allerdings keine echten Zoll-Werte, sondern Äquivalente zu historischen Röhrenkameras mit 1 Zoll-Glasröhre Außendurchmesser.
1/1" 9,6 mm × 12,8 mm 16,0 mm (diagonal)
2/3" 6,6 mm × 8,8 mm 11,0 mm
1/1,8" 5,1 mm × 6,8 mm 8,5 mm
1/2" 4,8 mm × 6,4 mm 8,0 mm
1/3" 3,6 mm × 4,8 mm 6,0 mm
y´= y * f´ / ( a - f´ )
Die Gegenstandsgröße y - Objektfeld
Die Gegenstandsgröße y ist in der Regel der zu erfassende Bereich, der mit der Kamera betrachtet werden muss. Auch dieser Wert ist normalerweise vorgegeben und bekannt, schließlich ist dies unser Prüfobjekt mit etwas Umgebung.
Einen Online-Assistenten zur Berechnung der Gegenstandsgröße finden Sie im Bereich "Service".
y= y´* ( a / f´-1 )
Die Brennweite f´ - "Objektivtype"
Die Brennweite wird in Millimetern angegeben und ist der Abstand zwischen dem optischen
Mittelpunkt eines Objektivs und dem Brennpunkt. In diesem Punkt schneiden sich alle Lichtstrahlen parallel einfallender Lichtstrahlen. Die Brennweite der Optik ist abhängig von der Brechkraft der Linse.
Mit der Brennweite f´ wird quasi das benötigte Objektiv errechnet und ist somit die wichtigste Angabe zur Charakterisierung eines entozentrischen Normal-Objektivs. Je größer der Wert der Brennweite, desto größere Teleeigenschaften weist es auf, kleine Brennweiten-Zahlen stehen für Weitwinkel- und Fisheye-Objektive. Generell neigen Objektive mit kurzer Brennweite zu stärkerer Verzeichnung als Optiken mit längerer Brennweite, sind aber meist lichtstärker und kompakter. Es kann generell empfohlen werden, eher bei größerem Arbeitsabstand mit längerer Brennweite zu arbeiten.
Einen Online-Assistenten zur Berechnung der Brennweite und anderer Werte finden Sie im Bereich "Service".
f' = a / ( y / y´ + 1 )
Beispiel:
Welche Brennweite ist nötig, um bei einem 1/2" Sensor und 300 mm Arbeitsabstand ein Bildfeld von 150mm zu erfassen?
y´ = 6,4 mm
y = 150 mm
a= 300 mm
f' = 300 / ( 150 / 6,4 + 1 ) = 12,3 mm
Die Brennweite f' beträgt 12,3 mm. In der Praxis werden Objektive mit 12 mm oder 12,5 mm Brennweite hergestellt und verkauft. Jetzt ist nur noch zu beachten, ob das Objektiv den qualitativen Anforderungen des Sensors entspricht (Standardoptik, Megapixel-Objektiv, farbkorrigierte Optik etc.) und ob das Objektiv in der Lage ist, den Sensor in seiner kompletten Größe zu belichten. C-Mount-Objektive sind zum Beispiel je nach Konstruktion in der Lage, maximal 1/2", 2/3" oder 1" -Sensoren etc. zu belichten. Ist der maximale Bildkreisdurchmesser der Optik kleiner als der des Sensors, treten starke Bildabschattungen am Rand (Vignettierung) auf.
Die Gegenstandsweite a - "Arbeitsabstand"
Die Gegenstandsweite bezeichnet den Abstand zwischen Gegenstand (Prüfobjekt) bis zur ersten Hauptebene des optischen Linsensystems. Der freie Arbeitsabstand zwischen Objekt und Vorderkante des Objektivs kann leider ohne nähere Kenntnisse der Optikkonstruktion nicht errechnet werden, ist aber bei industriellen C-Mount-Objektiven meistens 2-4 Zentimeter geringer.
Einen Online-Assistenten zur Berechnung des Arbeitsabstandes finden Sie im Bereich "Service".
a= f´ * ( y / y´ +1 )
Beispiel:
Welcher Arbeitsabstand wird benötigt, um mit einer 16mm-Optik an einer 1/3"-Kamera ein Objektfeld von 100mm zu erfassen?
y´ = 4,8 mm
y = 100 mm
f´= 16mm
a= 16mm * ( 100mm / 4,8mm +1)
a= 350mm
Der Abbildungsmaßstab β
Für telezentrische Messobjektive oder Makro-Objektive wird im Normalfall keine Brennweite angegeben, mit der man rechnen und zur Auswahl der Optik benutzen könnte. Diese Objektivtypen werden durch den Abbildungsmaßstab β (beta) charakterisiert. er ist sehr einfach zu errechnen.
Einen Online-Assistenten zur Berechnung des Abbildungsmaßstabes finden Sie im Bereich "Service".
β= y´ / y
Beispiel:
Ein telezentrisches Objektiv hat den Abbildungsmaßstab β=0,1. Dies entspricht in Bruchschreibweise 1/10. Mit einer Kamera mit 1/2" Sensor mit 6,4x 4,8mm Größe kann also ein Objekt von 64 x 48mm erfasst werden. Wird dasselbe Objektiv mit einer Kamera mit 1/3"-Sensor benutzt, können nur 48 x 36mm inspiziert werden.
Der Öffnungswinkel 2w
Entozentrische Objektive haben einen festen Öffnungswinkel. Daher kann durch Vergrößerung oder Verkleinerung des Arbeitsabstandes das zu betrachtende Objektfeld vergrößert oder verkleinert werden.
Einen Online-Assistenten zur Berechnung des Öffnungswinkels finden Sie im Bereich "Service".
2w = 2 * arctan ( y´ / 2 * 1 / f´ ) (in rad)
Ist der Öffnungswinkel sehr groß, muss üblicherweise mit starken Verzeichnungen der Optik gerechnet werden. Für viele Applikationen ist es daher ratsam, ein Objektiv mit längerer Brennweite zu wählen und dafür den Arbeitsabstand zu vergrößern, um den perspektivischen (Mess-)Fehler möglichst gering zu halten.
Auf der anderen Seite können mit extremen Weitwinkel-Optiken (Fisheye-Objektive, sowie Endoskope) spezielle Inspektionsaufgaben gelöst werden. Bei kleinen Arbeitsabständen kann so die seitliche Wand eines Bauteils, eine Senkung oder Bohrung inspiziert werden.






