Principle of triangulation - basics for machine vision
The laser line is directed to the surface at an oblique angle. It incides on the surfaces and creates a visible line. In areas where the object is lower, the beam is slightly shifted. By means of a camera this displacement of the bright laser lines can be determined in the image.
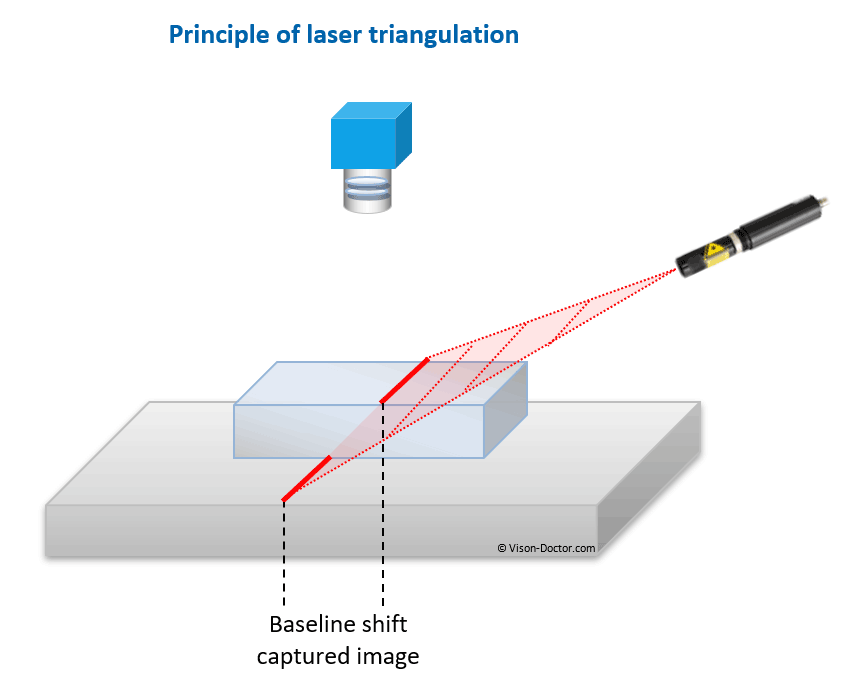 |
If the angle between camera and laser and the line displacement is known, the component height can be calculated using simple trigonometric formulae (right-angled triangle):
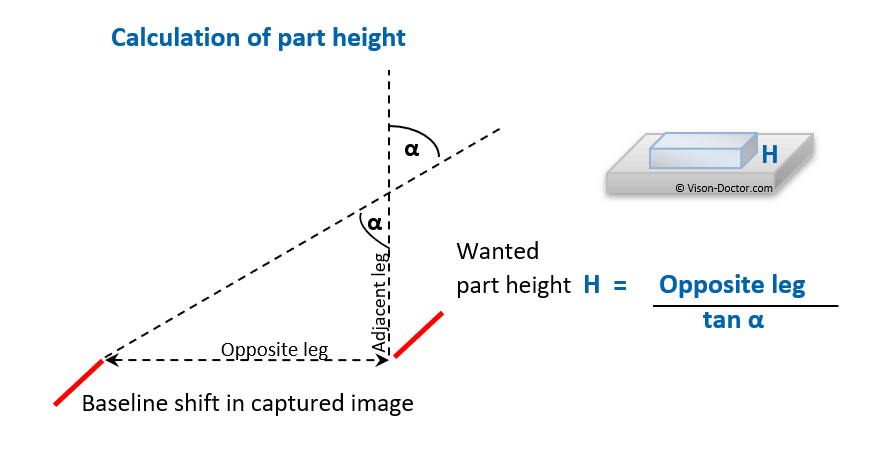 |
If the laser incides on the object at a shallow angle, even smallest differences in height cause a strong displacement of the lines, however, the detected height range is low. Even differences of tenths of millimetres can be detected easily in practice without special effort. In case of obtuse angles, the measuring accuracy is low, but large differences in height can be detected.
Square shape
Rounded edges
The principle of laser triangulation is brought to perfection when using 3D triangulation cameras and lasers. For this purpose the test object is continuously moved along a camera-laser system and a large number of triangulation profiles are generated. From the deflection of the single line profiles, a three-dimensional image of the object can be calculated using complex software algorithms.
Laser and speckle phenomena
Problems in the evaluation of laser lines and other projection patterns can be caused by so-called "speckles". This term describes the granular, glittering-looking light speckles which appear at rough surfaces of paper, wood, plastics and metals. The reason is the coherent light of the laser, with the light waves all oscillating into the same direction and with the same frequency and phase. The irregularities and surface textures result in the reflection of the coherent laser light and at the same time a shifting of the light phases. These overlapping leads to three-dimensional interference which is increasingly perceived by the human eye, since it constantly moves. Yet it is still clearly visible in the camera image, too.
A laser line is therefore no longer depicted as a sharp line, but a speckled, blurred line. In case of measuring applications or 3D triangulation systems, this can impair the subsequent image processing.
Superluminescence laser diodes can reduce the time consistency of the light, which results in fewer speckles. This, in turn, leads to more homogeneous and sharper lines and thus to a better evaluation. Do use low-speckle lasers for high-resolution applications!









